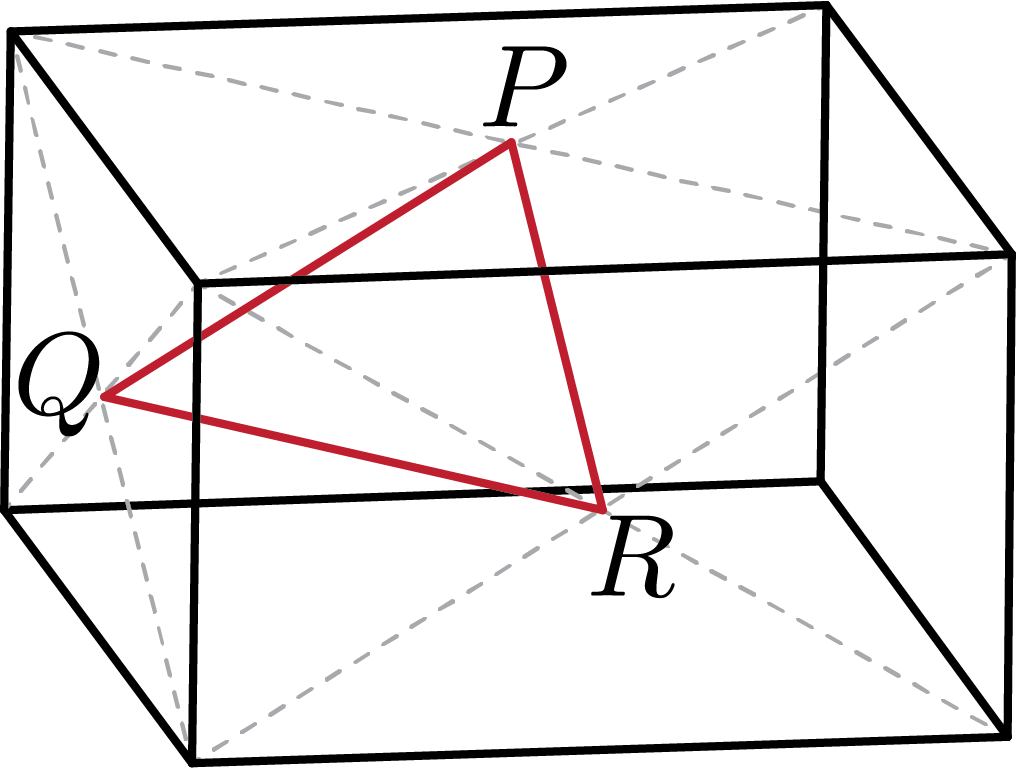

A rectangular prism is placed on a table. Points \(P\), \(Q\), and \(R\) lie on three different faces of the prism with \(P\) on the top face and \(Q\) and \(R\) on two adjacent side faces. Each point is located where the diagonals of the particular face intersect. Connecting these three points gives us \(\triangle PQR\).

If \(PQ=4\) cm, \(QR=5\) cm, and \(RP=6\) cm, determine the volume of the rectangular prism.
First, we label the top edge of the face containing point \(Q\) as \(AB\) and its midpoint as \(M\). Let \(AM = a\), \(PM=b\), and \(MQ = c\). Since the centre of a rectangle is where its diagonals intersect, \(P\) and \(Q\) are at the centres of their respective faces. Further, since the centre of a rectangle is also where the perpendicular bisectors of the sides of the rectangle meet, the rectangular prism has dimensions \(2a\), \(2b\), and \(2c\), as shown in the following diagram.

Since \(\angle{PMQ}=90^\circ\), it follows that \[b^2+c^2=16 \tag{1}\] Similarly, we can conclude the following. \[a^2+c^2=36\tag{2}\] \[a^2+b^2=25\tag{3}\] Adding equations \((1)\), \((2)\), and \((3)\) gives us the following. \[\begin{align*} 2a^2+2b^2+2c^2&=77\\ a^2+b^2+c^2&=\frac{77}{2} \tag{4}\end{align*}\]
Now, we subtract each of equations \((1)\), \((2)\), and \((3)\) from equation \((4)\) to obtain \[a^2=\frac{45}{2},~b^2=\frac{5}{2},~\text{and}~c^2=\frac{27}{2}\] Multiplying \(a^2,~b^2,\) and \(c^2\) together gives the product \[a^2b^2c^2=\frac{45}{2}\times\frac{5}{2}\times\frac{27}{2}=\frac{6075}{8}\]
Then, taking the positive square root, \[abc=\sqrt{\frac{6075}{8}}=\frac{45\sqrt{3}}{2\sqrt{2}}=\frac{45\sqrt{3}}{2\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}=\frac{45\sqrt{6}}{4}\]
To determine the volume of the rectangular prism, we multiply the side lengths together. \[\begin{aligned} V&=(2a)(2b)(2c)\\ &=8abc\\ &=8\left(\frac{45\sqrt{6}}{4}\right)\\ &=90\sqrt{6}~\text{cm}^3\end{aligned}\]
Therefore, the volume of the rectangular prism is \(90\sqrt{6}~\text{cm}^3\).