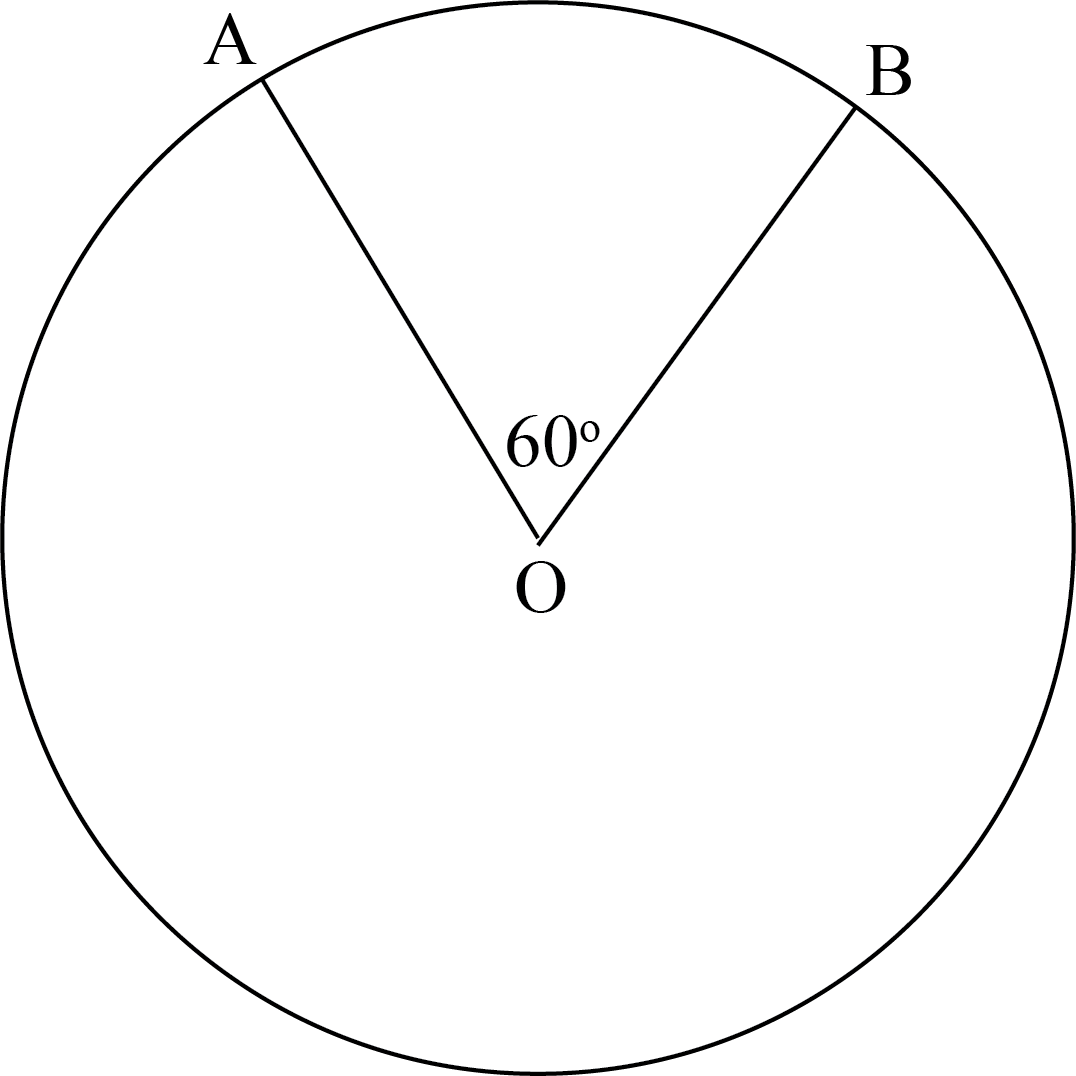

Points \(A\) and \(B\) are on a circle with centre \(O\) and radius \(6\) cm, such that \(\angle AOB=60 \degree\).

Determine the radius of the circle which passes through points \(A,~B,\) and \(O\).
Let \(C\) be the centre of the circle that passes through \(A\), \(B\), and \(O\). Then \(CA\), \(CB\), and \(CO\) are radii. Therefore, \(CA=CB=CO=r\), where \(r\) is the radius of the circle.
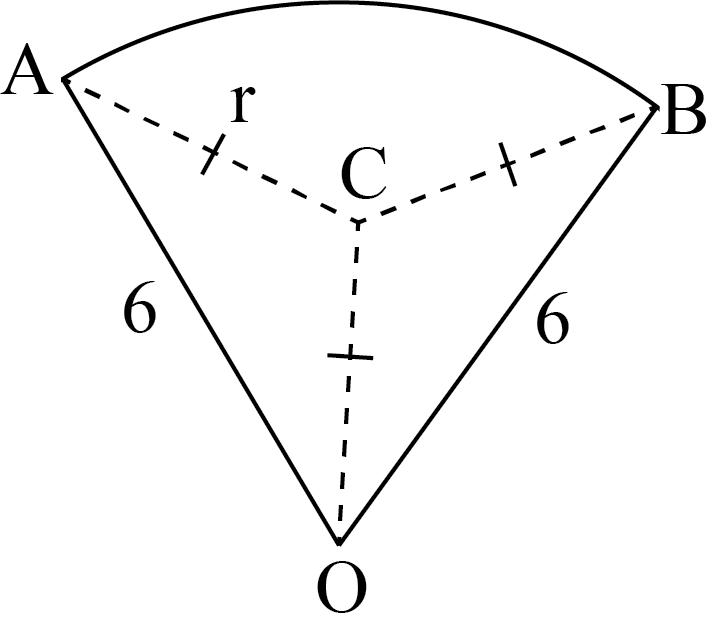
In \(\triangle CAO\) and \(\triangle CBO\), \(CA=CB\), \(CO\) is common, and \(OA=OB\). Therefore, \(\triangle CAO \cong \triangle CBO\) and it follows that \(\angle COA=\angle COB\). But \(\angle AOB=60\degree\). Therefore, \(\angle COA=\angle COB=30\degree\).
In \(\triangle CAO\), \(CA=CO=r\) and \(\triangle CAO\) is isosceles. Therefore, \(\angle CAO=\angle COA=30\degree\) and \(\angle ACO=180\degree-30\degree-30\degree=120\degree\).
From here we can find the length of \(r\) using either the sine law or the cosine law.
Method 1: Using the sine law, \[\begin{aligned} \dfrac{CA}{\sin{(\angle COA)}}&=\dfrac{OA}{\sin{(\angle ACO)}}\\ \dfrac{r}{\sin{30\degree}}&=\dfrac{6}{\sin{120\degree}}\\ r&=\dfrac{6}{\sin{120\degree}}\times \sin{30\degree}\\ r&=\dfrac{6}{\frac{\sqrt{3}}{2}}\times \frac{1}{2}\\ r&=6\times \frac{2}{\sqrt{3}} \times \frac{1}{2}\\ r&=\frac{6}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}\\ r&=2\sqrt{3}\text{ cm}\end{aligned}\] Therefore, the radius of the circle that passes through \(A,~B,\) and \(O\) is \(2\sqrt{3}\) cm.
Method 2: Using the cosine law, \[\begin{aligned} CA^2&=CO^2+AO^2-2\times CO\times AO\times \cos{(\angle COA)}\\ r^2&=r^2+6^2-2(6)(r)\cos{30\degree}\\ 12r\cos{30\degree}&=36\\ r\cos{30\degree}&=3\\ r\times \frac{\sqrt{3}}{2}&=3\\ r\times \sqrt{3}&=6\\ r\times \sqrt{3}\times \sqrt{3}&=6\times \sqrt{3}\\ 3r&=6 \sqrt{3}\\ r&=2 \sqrt{3}\text{ cm}\end{aligned}\] Therefore, the radius of the circle that passes through \(A,~B,\) and \(O\) is \(2\sqrt{3}\) cm.