

Kenna likes making artistic creations using parabolas, to put on the walls of her math classroom. She drew a parabola with vertex \(E(7,9)\) and plotted points \(A(9,8)\) and \(B(3,b)\) on the parabola as well as points \(C\) and \(D\) where the parabola intersects the \(x\)-axis, with \(C\) to the left of \(D\). Then she connected points \(A\), \(B\), \(C\), and \(D\) to form quadrilateral \(ABCD\), and painted it blue. What is the area of quadrilateral \(ABCD\)?

First we need to find the equation of the parabola. Then, we can find the \(x\)-intercepts of the parabola and the \(y\)-coordinate of point \(B\) on the parabola.
We are given the vertex of the parabola, \(E(7,9)\). Using the vertex form of the equation of a parabola, \(y=a(x-h)^2+k\), with vertex \((h,k)=(7,9)\), the equation of the parabola is \(y=a(x-7)^2+9\).
Since the point \(A(9,8)\) is on the parabola, we can substitute \((x,y)=(9,8)\) into the equation \(y=a(x-7)^2+9\) to find the value of \(a\). \[\begin{aligned} 8&=a(9-7)^2+9\\ 8&=a(4)+9\\ -1&=4a\\ -\frac{1}{4}&=a\end{aligned}\] The equation of the parabola is therefore \(y=-\frac{1}{4}(x-7)^2+9\).
To find the \(y\)-coordinate of \(B(3,b)\), we substitute \((x,y)=(3,b)\) into the equation of the parabola. \[\begin{aligned} b&=-\frac{1}{4}(3-7)^2+9\\ &=-\frac{1}{4}(16)+9\\ &=-4+9\\ &=5\end{aligned}\]
Therefore, the coordinates of \(B\) are \((3,5)\).
To find the \(x\)-intercepts of the parabola, we substitute \(y=0\) into the equation of the parabola. \[\begin{aligned} 0&=-\frac{1}{4}(x-7)^2+9\\ -9&=-\frac{1}{4}(x-7)^2\\ 36&=(x-7)^2\\ \pm 6&=x-7\end{aligned}\] It follows that \(x-7=-6\) or \(x-7=6\). Then the \(x\)-intercepts of the parabola are 1 and 13. Therefore, the coordinates of \(C\) and \(D\) are \(C(1,0)\) and \(D(13,0)\).
Now that we know the coordinates of \(A\), \(B\), \(C\), and \(D\), we can calculate the area of quadrilateral \(ABCD\). There are many ways to do this. We will proceed as follows.
From \(B(3,5)\) and \(A(9,8)\), drop perpendiculars, intersecting the \(x\)-axis at \(F(3,0)\) and \(G(9,0)\), respectively. From \(B(3,5)\) draw a line perpendicular to \(AG\), intersecting \(AG\) at \(H(9,5)\). Draw line segment \(BG\).
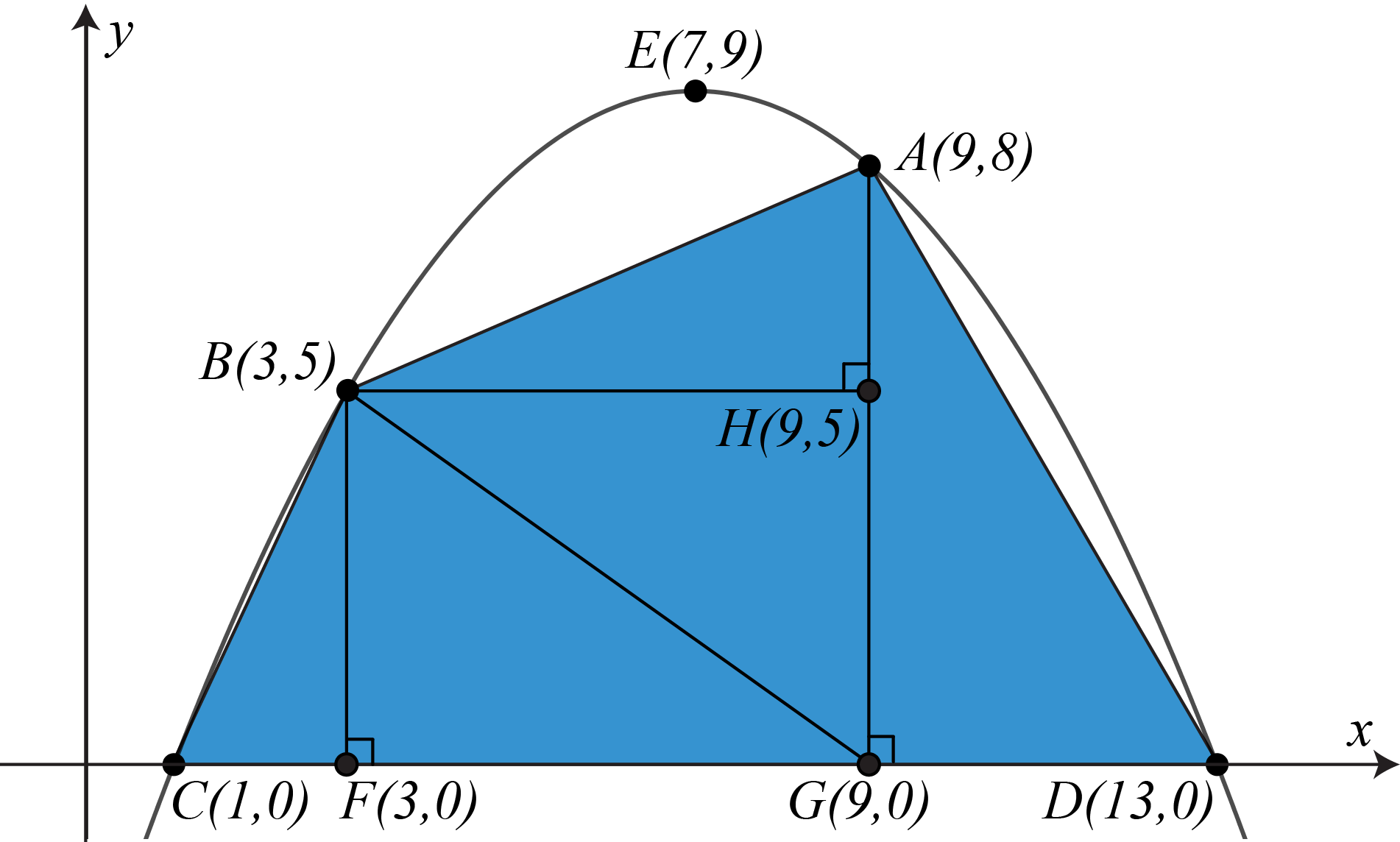
Note that line segments \(BG\) and \(AG\) divide the quadrilateral into three regions: \(\triangle CGB\), \(\triangle AGD\), and \(\triangle AGB\).
We will use the coordinates of the points to find the lengths of several horizontal and vertical line segments that will be required for the area calculation. \[BH=9-3=6,\ CG=9-1=8,\ GD=13-9=4,\ BF=5-0=5,\text{ and }AG=8-0=8.\]
To determine the area of \(ABCD\), we will find the sum of the areas of \(\triangle CGB\), \(\triangle AGD\) and \(\triangle AGB\). \begin{align*} \text{Area }ABCD&=\text{Area }\triangle CGB+\text{Area }\triangle AGD+\text{Area }\triangle AGB\\ &=\frac{CG\times BF}{2}+\frac{AG\times GD}{2}+\frac{AG\times BH}{2}\\ &=\frac{8\times 5}{2}+\frac{8\times 4}{2}+\frac{8\times 6}{2}\\ &=20+16+24\\ &=60\text{ units}^2 \end{align*} Therefore, the area of quadrilateral \(ABCD\) is \(60\text{ units}^2.\)