Three circles are contained in a rectangle. Two of the circles have a radius of \(1\) and one of the circles has a radius of \(2\). The larger circle is tangent to three sides of the rectangle. The two smaller circles are each tangent to the larger circle and tangent to each other, and they are also each tangent to two sides of the rectangle. Determine the area of the rectangle that is not covered by the circles.

Note: For this problem, the following known results about circles may be useful:
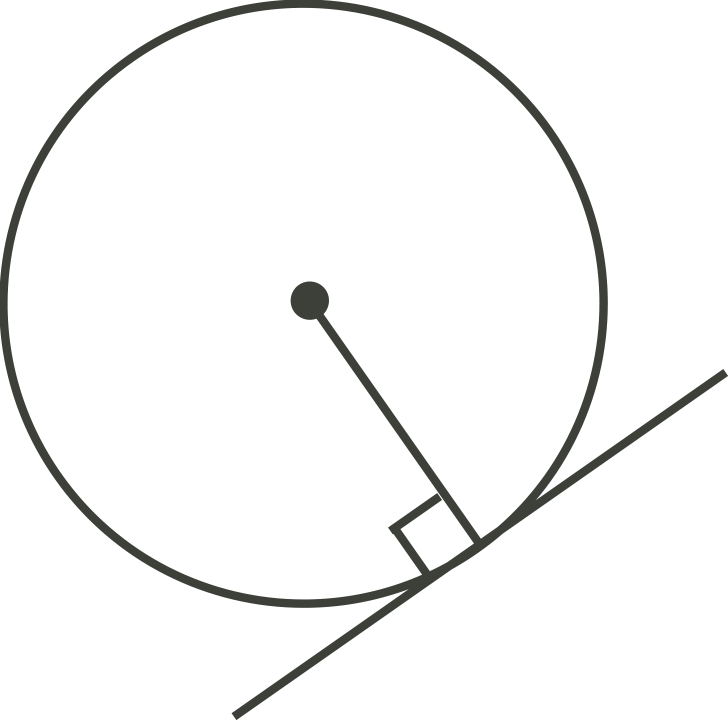
If a line is tangent to a circle, then the line is perpendicular to the radius drawn to the point of tangency.
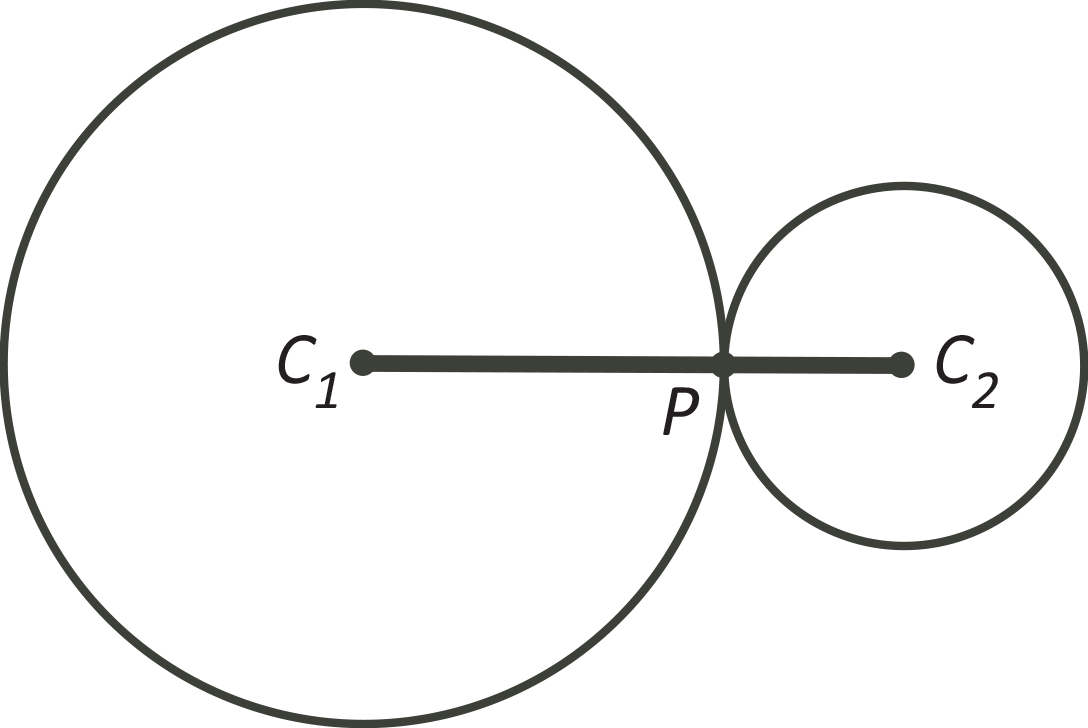
If two circles are tangent to each other at point \(P\), then a line segment through the point of tangency can be drawn connecting the two centres, \(C_1\) and \(C_2\).