

Three circles are contained in a rectangle. Two of the circles have a radius of \(1\) and one of the circles has a radius of \(2\). The larger circle is tangent to three sides of the rectangle. The two smaller circles are each tangent to the larger circle and tangent to each other, and they are also each tangent to two sides of the rectangle. Determine the area of the rectangle that is not covered by the circles.

Note: For this problem, the following known results about circles may be useful:
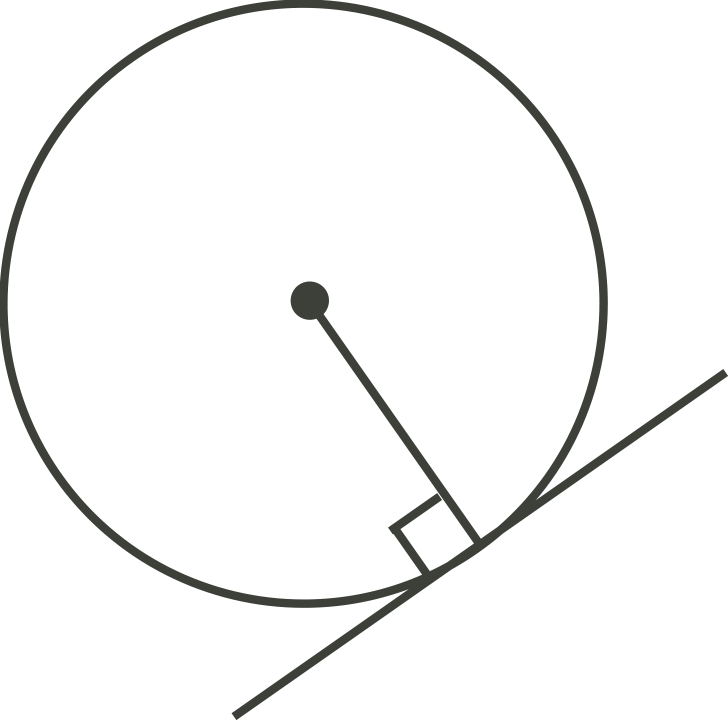
If a line is tangent to a circle, then the line is perpendicular to the radius drawn to the point of tangency.
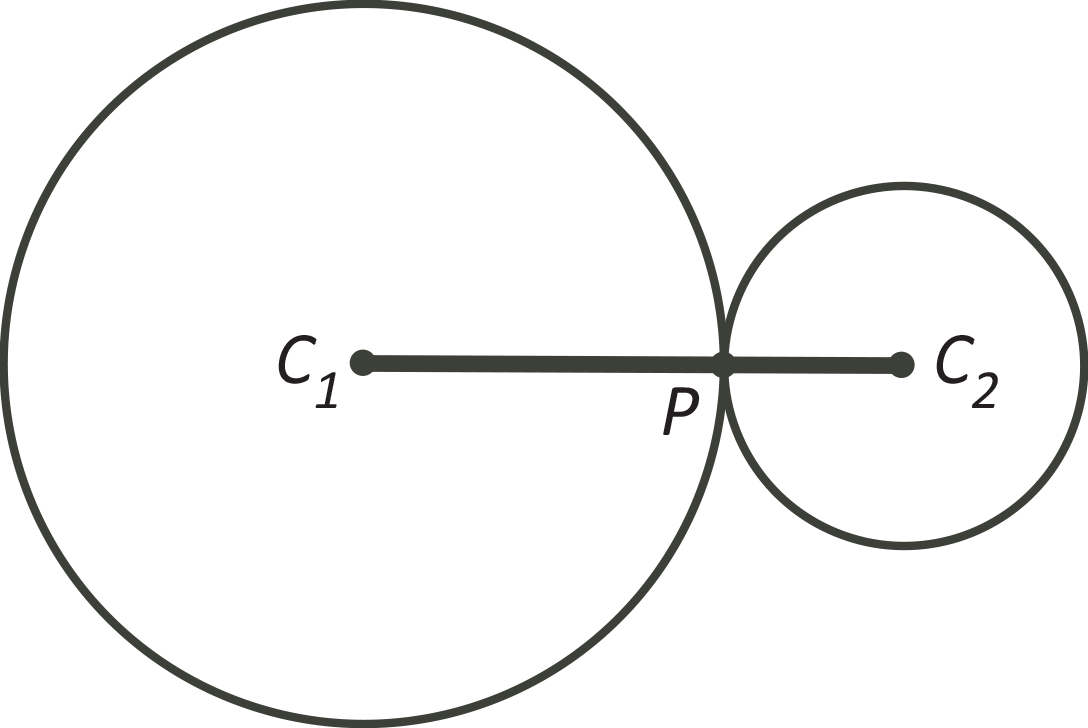
If two circles are tangent to each other at point \(P\), then a line segment through the point of tangency can be drawn connecting the two centres, \(C_1\) and \(C_2\).
Let the centre of the larger circle be \(B\) and the centre of one of the smaller circles be \(E\). Let \(C\) be the point of tangency of the two smaller circles. Let \(F\) be the point of tangency of the larger circle and the smaller circle with centre \(E\). Position line segment \(AD\) so that it is parallel to the longer side of the rectangle, such that \(A\) and \(D\) are midpoints of the shorter sides of the rectangle and \(A\) lies on the larger circle. \(AD\) will pass through \(B\) and \(C\).
Since the larger circle is tangent to two opposite sides of the rectangle and its radius is \(2\) m, then the length of the shorter side of the rectangle is equal to the diameter of the larger circle, or \(4\) m.
Let the length of the longer side of the rectangle be \(d\). This is also the length of \(AD\). We know that \(AB=2\) m, the length of a radius of the larger circle, and \(CD=1\) m, the same length as a radius of a smaller circle. We need to find the length of \(BC\).
Since \(AD\) is tangent to the smaller circles at \(C\), we know that \(EC\) is a radius of one of the smaller circles and is perpendicular to \(AD\) at \(C\). Since the circles with centres \(B\) and \(E\) are tangent at \(F\), \(EFB\) is a straight line segment and \(EB=EF+FB=1+2=3\) m.
Combining this information, \(\triangle ECB\) is right-angled at \(C\).
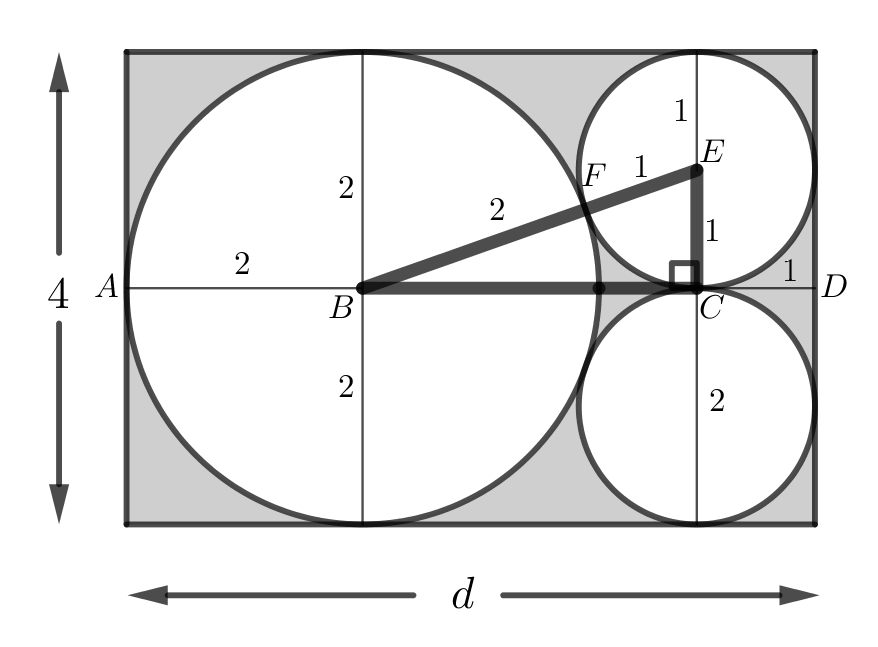
Using the Pythagorean Theorem in \(\triangle ECB\), we have \(BC^2=EB^2-EC^2=3^2-1^2=8\). Thus, \(BC=\sqrt{8}\), since \(BC > 0\).
Therefore, the length of the longer side of the rectangle is \[\begin{aligned} d&=AB+BC+CD\\ &=2+\sqrt{8}+1\\ &=3+\sqrt{8}\end{aligned}\]
To find the area not covered by the circles, we find the area of the rectangle and subtract the areas of the three circles. \[\begin{aligned} \text{Shaded Area}&=\text{Area of Rectangle}-\text{Area of larger circle}-\text{Area of two smaller circles}\\ &=4\times (3+\sqrt{8}) - \pi\times 2^2-2\times (\pi \times 1^2)\\ &=12+4\sqrt{8}-4\pi-2\pi\\ &=12+4\sqrt{8}-6\pi\end{aligned}\]
Students who have learned to simplify radicals will know that \(\sqrt{8}=\sqrt{4}\sqrt{2}=2\sqrt{2}\). Therefore, the shaded area can then be written \(12+4\times 2\sqrt{2}-6\pi=12+8\sqrt{2}-6\pi\).
Therefore, the area of the rectangle not covered by the circles is \((12+4\sqrt{8}-6\pi)\mbox{ m}^2\) or \((12+8\sqrt{2}-6\pi)\mbox{ m}^2\), which is approximately \(4.5\mbox{ m}^2\).