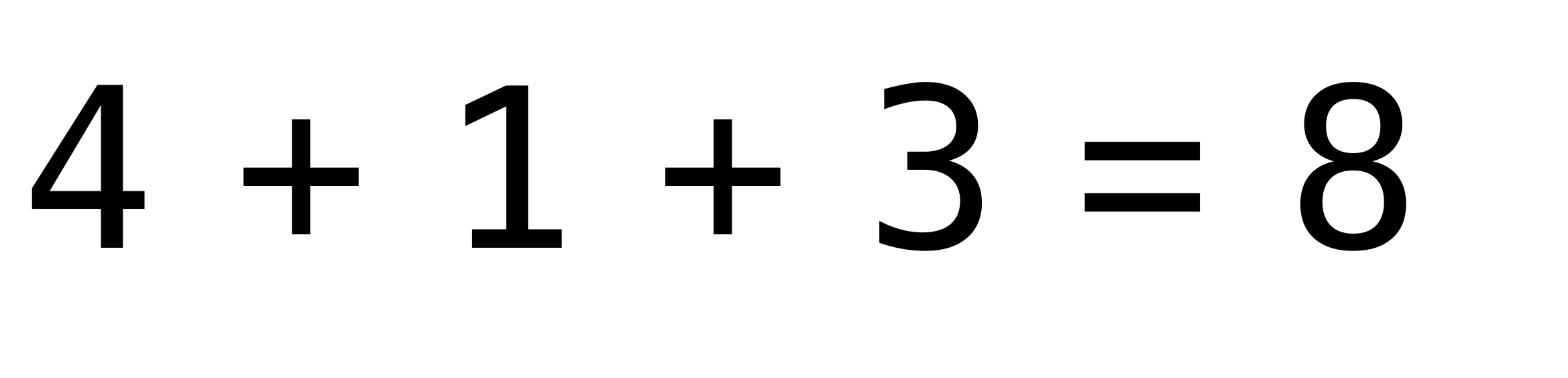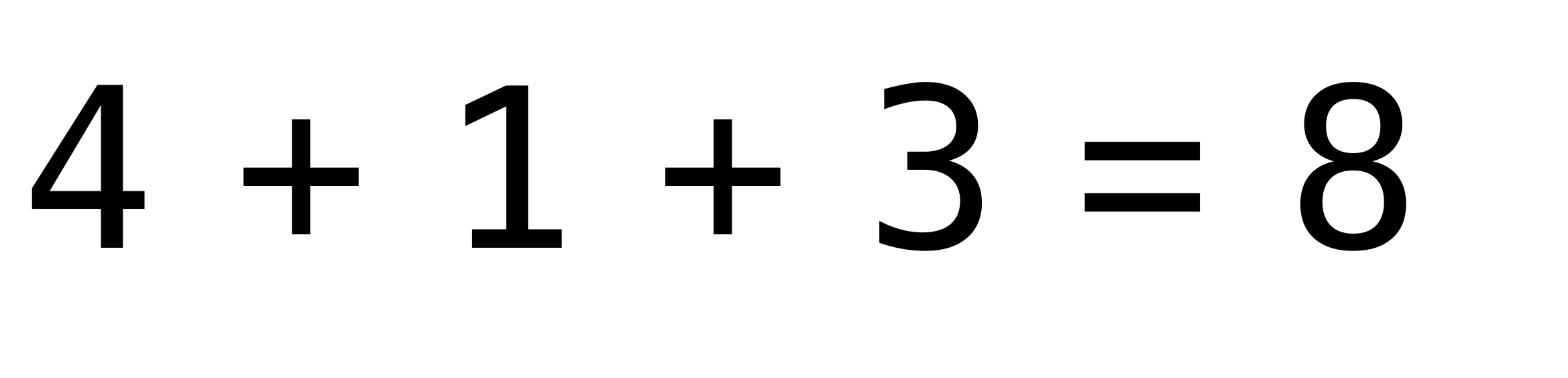

The digit sum of a positive integer is found by summing its digits.
The digital root is found by repeatedly calculating the digit sum until a single digit is achieved.
The digit sum of \(413\) is \(8\), since \(4+1+3=8\) and \(8\) is a single-digit number. Note that the digital root is also \(8\), and this is calculated in one step.
The digit sum of 642 is \(6+4+2=12\), which is not a single-digit number. The digit sum of \(12\) is \(1+2=3\), which is a single-digit number. Therefore, the digital root of \(642\) is \(3\). This is calculated in two steps.
The digital root of \(4\) is \(4\). This is calculated in zero steps.
How many three-digit numbers have a digital root of \(5\) that is calculated in three or fewer steps?