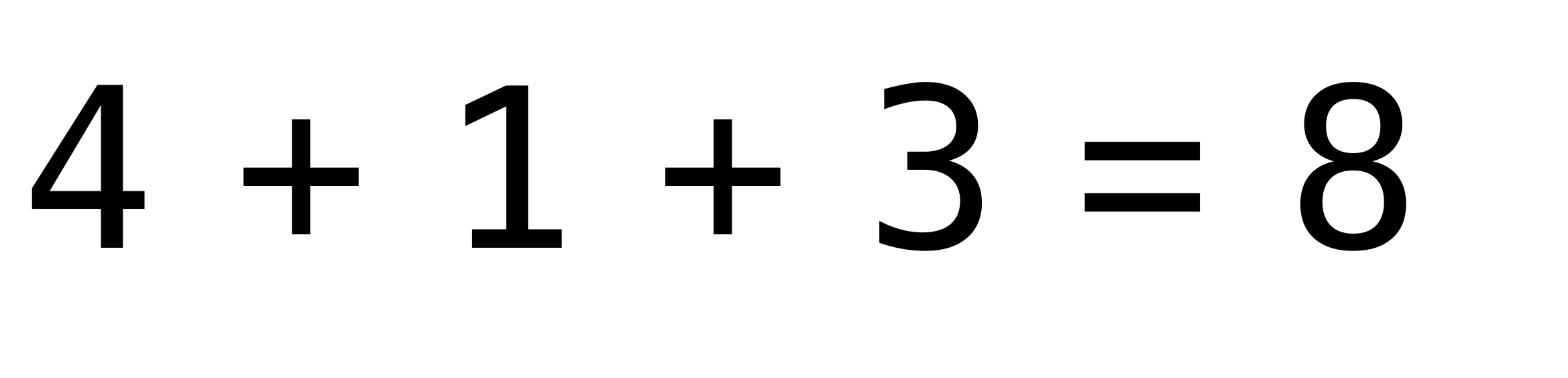

The digit sum of a positive integer is found by summing its digits.
The digital root is found by repeatedly calculating the digit sum until a single digit is achieved.
The digit sum of \(413\) is \(8\), since \(4+1+3=8\) and \(8\) is a single-digit number. Note that the digital root is also \(8\), and this is calculated in one step.
The digit sum of 642 is \(6+4+2=12\), which is not a single-digit number. The digit sum of \(12\) is \(1+2=3\), which is a single-digit number. Therefore, the digital root of \(642\) is \(3\). This is calculated in two steps.
The digital root of \(4\) is \(4\). This is calculated in zero steps.
How many three-digit numbers have a digital root of \(5\) that is calculated in three or fewer steps?
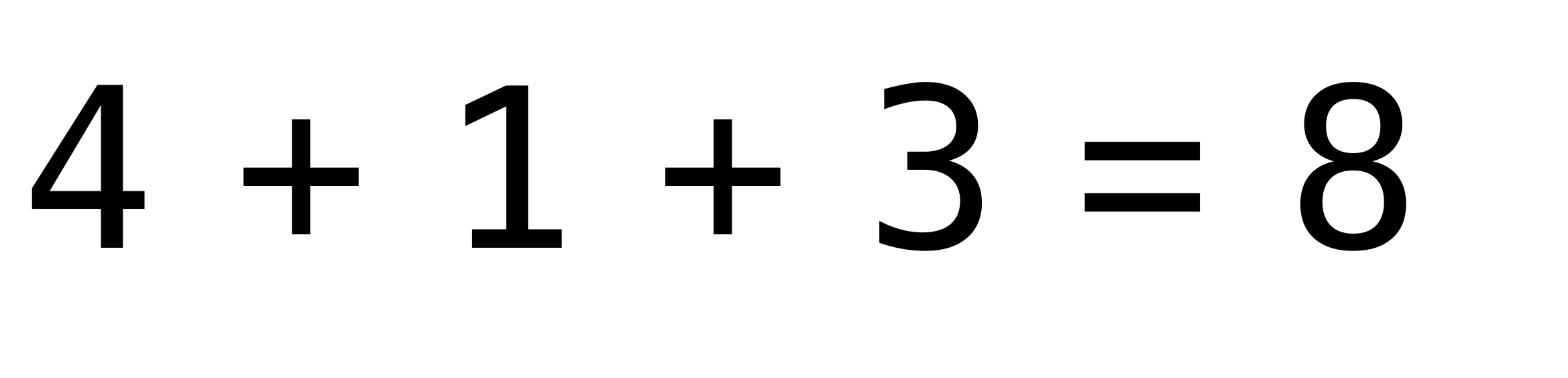
We will consider four cases for the three-digit numbers: a digital root of \(5\) in zero steps, a digital root of \(5\) in one step, a digital root of \(5\) in two steps, and a digital root of \(5\) in three steps.
Case 1: A digital root of \(5\) that is reached in zero steps.
This only occurs when the number is \(5\), which is not a three-digit number.
There are no three-digit numbers with a digital root of \(5\) that can be reached in zero steps.
Case 2: A digital root of \(5\) that is reached in one step.
Since the digital root is \(5\), then no digit in the three-digit number can be higher than \(5\). We use this to carefully generate the list below of all of the three-digit numbers whose digits sum to \(5\).
\(104\), \(113\), \(122\), \(131\), \(140\)
\(203\), \(212\), \(221\), \(230\)
\(302\), \(311\), \(320\)
\(401\), \(410\)
\(500\)
There are \(5+4+3+2+1=15\) three-digit numbers with a digital root of \(5\) that can reached in exactly one step.
Case 3: A digital root of \(5\) that is reached in two steps.
The maximum sum of the digits of a three-digit number is \(9+9+9=27\). In order to reach a digital root of \(5\) in two steps, the initial sum must be a two-digit number less than \(28\) whose digits sum to \(5\). There are only \(2\) two-digit numbers that satisfy this condition, namely \(14\) and \(23\).
If the sum of the digits of the three-digit number is \(14\), we can systematically generate the possible numbers. For example, if the first digit is \(1\), then the other two digits add to \(13\). This happens exactly when the last two digits are \(4\) and \(9\), \(5\) and \(8\), or \(6\) and \(7\). The resulting six three-digit numbers with first digit \(1\) are shown on the first line below. The remaining lines are generated in a similar manner and are also shown below.
\(149\), \(158\), \(167\), \(176\), \(185\), \(194\)
\(239\), \(248\), \(257\), \(266\), \(275\), \(284\), \(293\)
\(329\), \(338\), \(347\), \(356\), \(365\), \(374\), \(383\), \(392\)
\(419\), \(428\), \(437\), \(446\), \(455\), \(464\), \(473\), \(482\), \(491\)
\(509\), \(518\), \(527\), \(536\), \(545\), \(554\), \(563\), \(572\), \(581\), \(590\)
\(608\), \(617\), \(626\), \(635\), \(644\), \(653\), \(662\), \(671\), \(680\)
\(707\), \(716\), \(725\), \(734\), \(743\), \(752\), \(761\), \(770\)
\(806\), \(815\), \(824\), \(833\), \(842\), \(851\), \(860\)
\(905\), \(914\), \(923\), \(932\), \(941\), \(950\)
There are \(6+7+8+9+10+9+8+7+6=70\) three-digit numbers with a digital root of \(5\) that can reached in exactly two steps with the initial sum of \(14\).
If the sum of the digits of the three-digit number is \(23\), we can again systematically generate the possible numbers. If the final two digits of the three-digit number are \(9\) and \(9\), the first digit must be a \(5\). Therefore, no three-digit number less than \(599\) has digits that sum to \(23\). (For example if one of the digits is \(4\), then the sum of the other two digits must be \(19\) and this is impossible using two single digits.) The list below is generated in a similar way to the one shown above.
\(599\)
\(689\), \(698\)
\(779\), \(788\), \(797\)
\(869\), \(878\), \(887\), \(896\)
\(959\), \(968\), \(977\), \(986\), \(995\)
There are \(1+2+3+4+5=15\) three-digit numbers with a digital root of \(5\) that can reached in exactly two steps with the initial sum of \(23\).
In total, there are \(70+15=85\) three-digit numbers with a digital root of \(5\) that can be reached in exactly two steps.
Case 4: A digital root of \(5\) that is reached in three steps.
The maximum sum of the digits of a three-digit number is \(27\). The only number from \(10\) to \(27\) whose digits add to a two-digit number is \(19\). The digit sum of \(19\) is \(10\), whose digit sum is \(1\), not \(5\). Therefore, no three-digit number exists that has a digital root of \(5\) that is reached in three steps. It follows that all three-digit numbers with a digital root of \(5\) can be reached in at most two steps.
The above cases represent the only possible ways for a three-digit number to have a digital root of \(5\). In total there are \(0+15+85+0=100\) three-digit numbers with a digital root of \(5\), all of which can be reached in two or fewer steps.