A Venn diagram has two circles, labelled A and B.
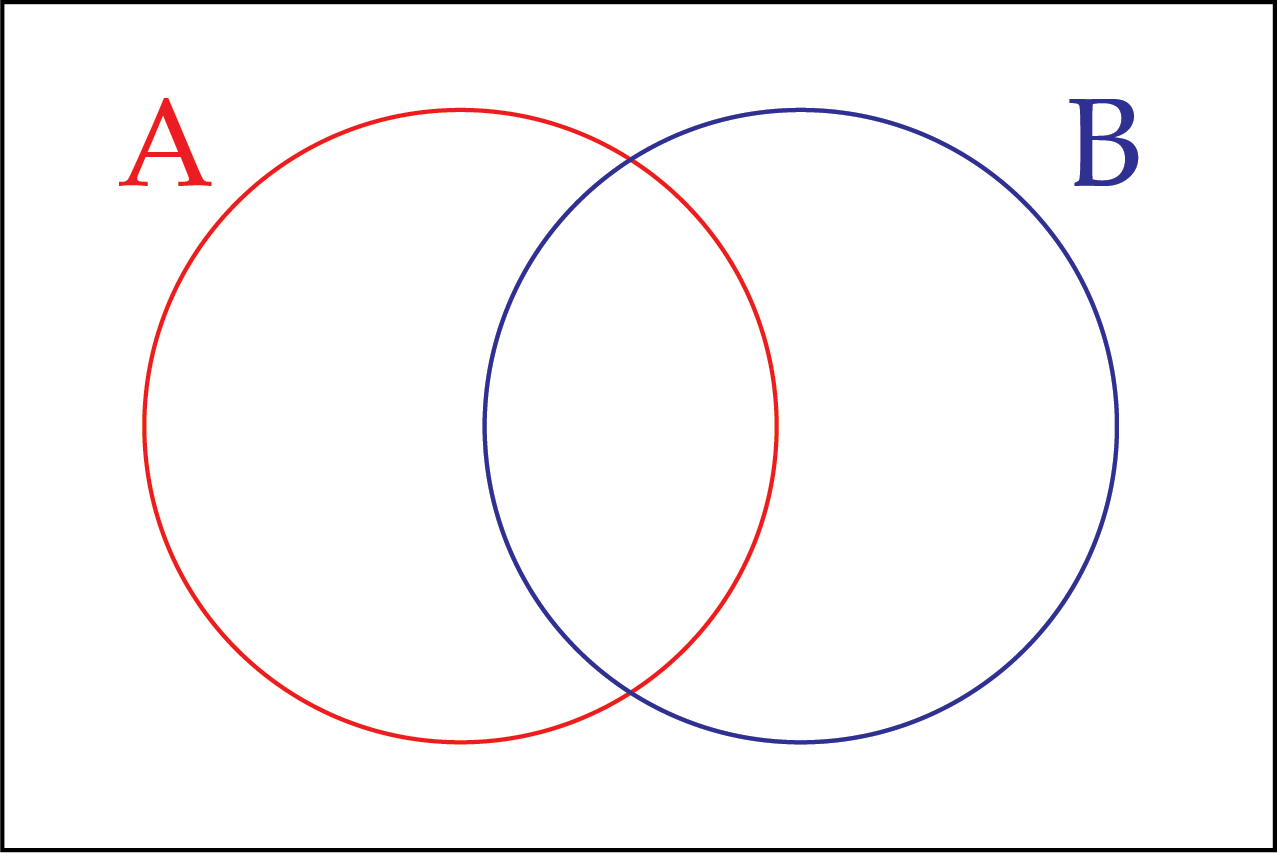
Each circle contains functions, \(f(x)\), that satisfy the following criteria.
A: \(f(2)=-3\)
B: \(f(-2)=-1\)
The overlapping region in the middle contains functions that are in both A and B, and the region outside both circles contains functions that are neither in A nor B.
In total this Venn diagram has four regions. Place functions in as many of the regions as you can. Is it possible to find a function for each region?
A Venn diagram has three circles, labelled A, B, and C.
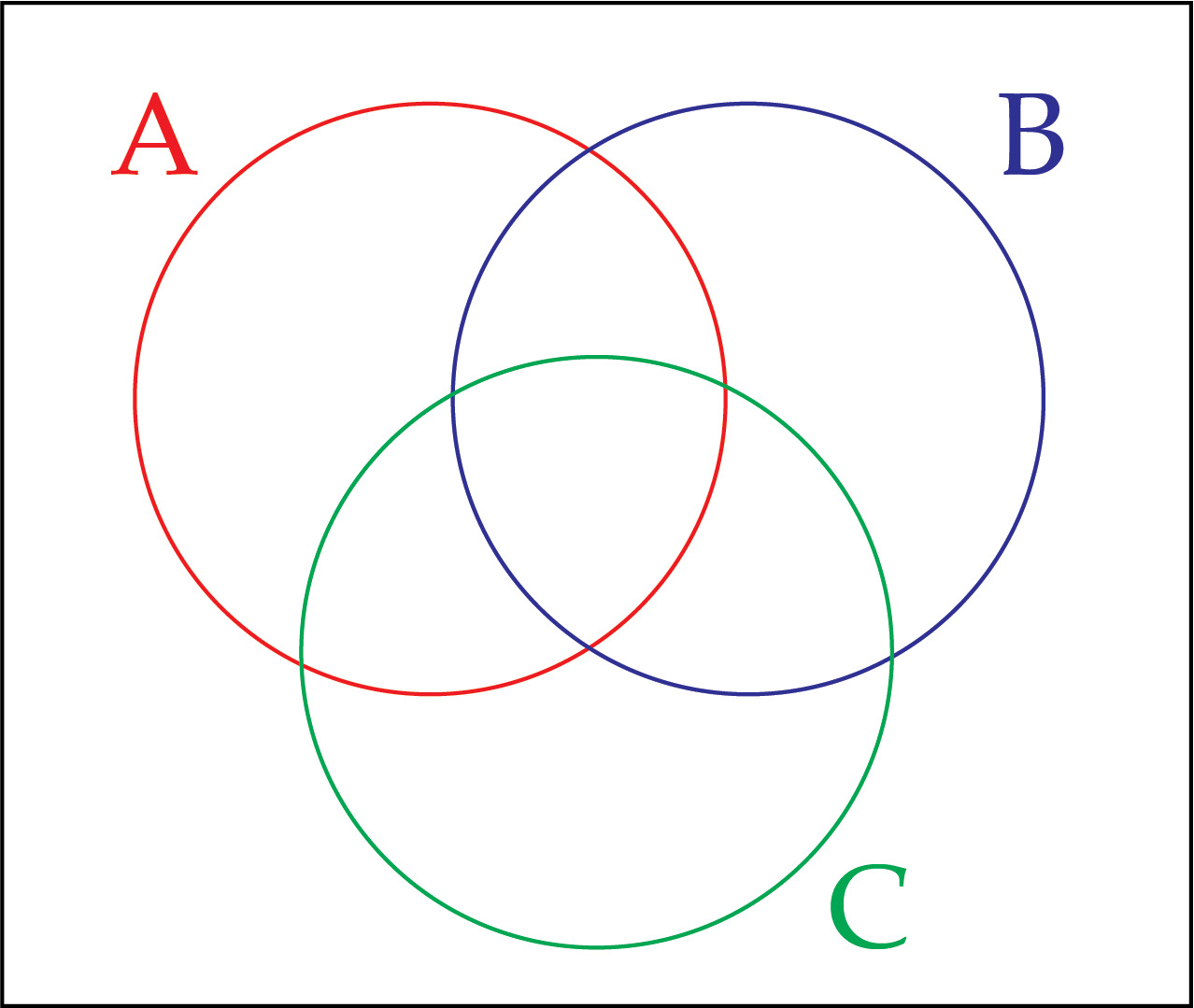
Each circle contains ordered pairs, \((x,y)\), where \(x\) and \(y\) are real numbers, that satisfy the following criteria.
A: \(y=(x+3)^3+2\)
B: \(y=\dfrac{1}{2}x^2+1\)
C: \(y=|x+1|\)
In total this Venn diagram has eight regions. Place ordered pairs in as many of the regions as you can. Is it possible to find an ordered pair for each region?
