


If vertices \(P\), \(Q\), and \(S\) are located at \((0,30)\), \((k,50)\) and \((40,0)\), respectively, and the area of \(PQRS\) is \(1340\text{ units}^2\), determine the coordinates of \(Q\) and \(R\).
Solution 1:
In this solution we will use a method known commonly as "completing the rectangle".
Since \(PQRS\) is a parallelogram, \(PQ=SR\) and \(PQ\) is parallel to \(SR\). We can use this to find the coordinates of \(R\). To get from \(P\) to \(Q\), we go up 20 units and right \(k\) units. Therefore, to get from \(S\) to \(R\) we do the same. Therefore, \(R\) is located at \((40+k,20)\).
Enclose \(PQRS\) in rectangle \(OTUV\) such that \(OT\) is on the positive \(y\)-axis passing through \(P\), \(TU\) is parallel to the positive \(x\)-axis passing through \(Q\), \(UV\) is parallel to the positive \(y\)-axis passing through \(R\), and \(OV\) lies along the positive \(x\)-axis passing through \(S\). The \(y\)-coordinate of \(Q\) is the distance from the \(x\)-axis to \(TU\) and also the height, \(UV\), of rectangle \(OTUV\). It follows that \(OT = UV=50\) units. Therefore, the coordinates of \(T\) are \((0,50)\). Similarly, the \(x\)-coordinate of \(R\) is the distance from the \(y\)-axis to \(UV\) and also the width, \(OV\), of rectangle \(OTUV\). It follows that \(TU = OV=(40+k)\) units. Therefore, the coordinates of \(V\) are \((40+k,0)\) and the coordinates of \(U\) are \((40+k, 50)\).
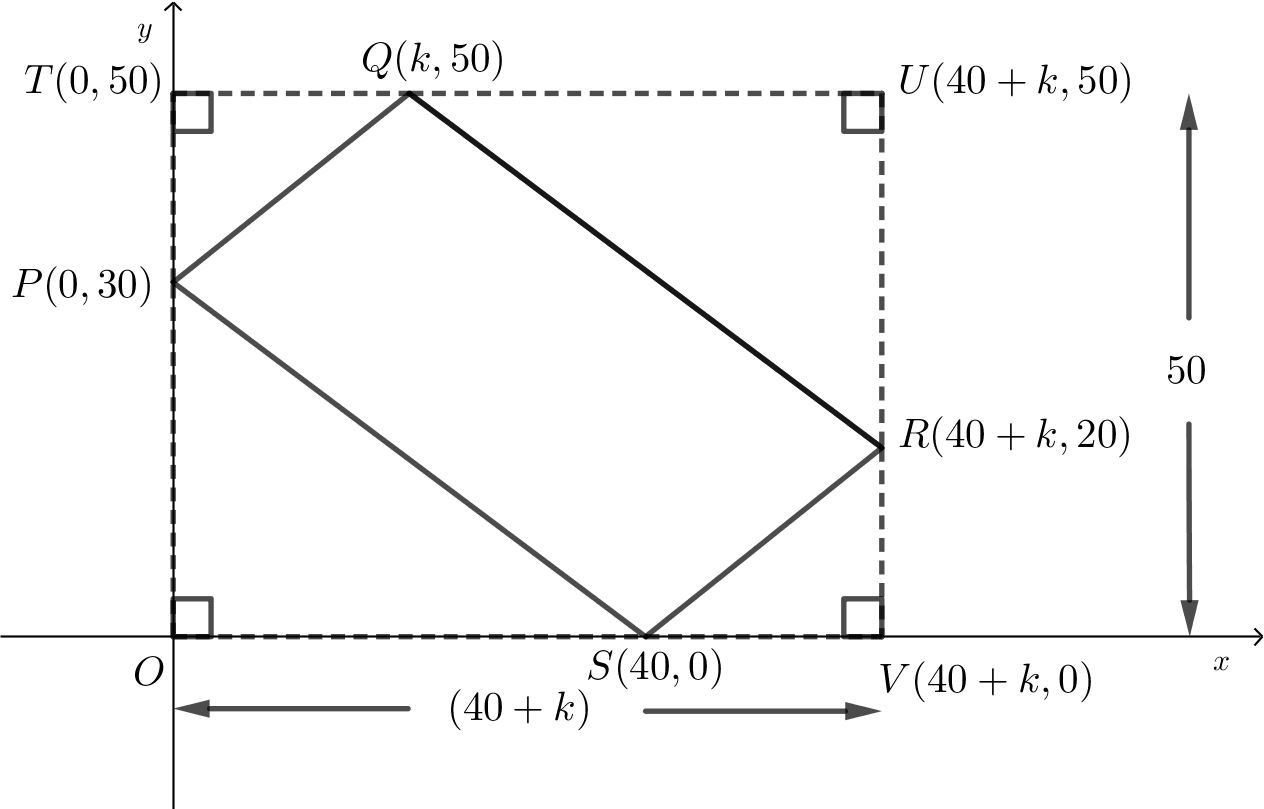
We can now put the information together using areas to determine the value of \(k\). \[\begin{aligned} \text{Area }OTUV&=\text{Area }\triangle PTQ+\text{Area }\triangle QUR+\text{Area }\triangle RVS+\text{Area }\triangle SOP+\text{Area }PQRS\\ UV\times OV&=\frac{PT\times TQ}{2}+\frac{QU\times UR}{2}\ +\frac{RV\times VS}{2}+\frac{OS\times OP}{2}\ +\ 1340\\ 50\times (40+k)&=\frac{(50-30)\times k}{2}+\frac{((40+k)-k)\times (50-20)}{2}+\frac{20\times ((40+k)-40)}{2}+\frac{40\times 30}{2}+1340\\ 50\times (40+k)&=\frac{20\times k}{2}+\frac{40\times 30}{2}\ +\frac{20\times k}{2}+\frac{40\times 30}{2}\ +\ 1340\\ 2000+50k&=10k+600+10k+600+1340\\ 2000+50k&=20k+2540\\ 30k&=540\\ k&=18\end{aligned}\]
Therefore, the value of \(k\) is \(18\) and coordinates of \(Q\) and \(R\) are \(Q(18,50)\) and \(R(58,20)\).
Solution 2:
In this solution we will use linear equations, intersections, and lengths to find \(k\).
Since \(PQRS\) is a parallelogram, \(PQ=SR\) and \(PQ\) is parallel to \(SR\). We can use this to find the coordinates of \(R\). To get from \(P\) to \(Q\), we go up 20 units and right \(k\) units. Therefore, to get from \(S\) to \(R\) we do the same. Therefore, \(R\) is located at \((40+k,20)\).
Construct a line perpendicular to \(PS\) that passes through \(Q\) and meets \(PS\) at \(W\).
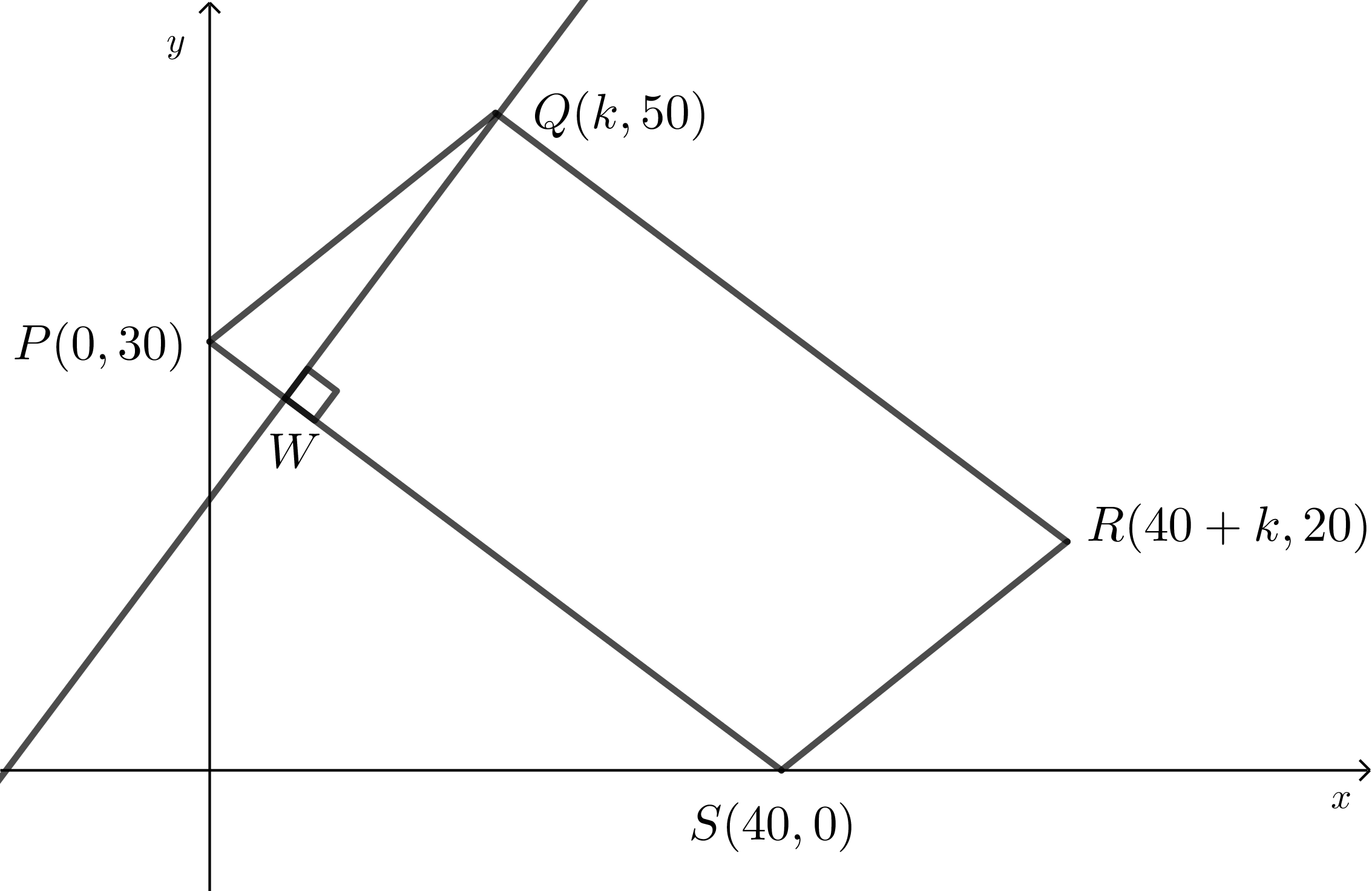
We are going to find the coordinates of \(W\) in terms of \(k\).
The line through \(PS\) has a slope of \(-\frac{3}{4}\) and a \(y\)-intercept of 30. Therefore, the equation of this line is \[y=-\frac{3}{4}x + 30 \tag{1}\]
The line though \(QW\) is perpendicular to \(PS\) and so has slope \(\frac{4}{3}\). The equation of this line is \(4x - 3y = C\). Substituting the coordinates of \(Q\) into this equation, we get \(4k - 3(50) = C\) or \(C = 4k -150\). Therefore, the line through \(QW\) has equation \[4x - 3y = 4k - 150\tag{2}\]
\(W\) is the intersection point of the lines with equations \((1)\) and \((2)\).
Substituting equation \((1)\) into equation \((2)\), we get: \[\begin{align*} 4x - 3\left(-\frac{3}{4}x + 30\right) &= 4k -150\\ 4x + \frac{9}{4}x - 90 &= 4k -150\\ 16x + 9x - 360 &= 16k -600\\ 25x &= 16k - 240\\ x &= 0.64k - 9.6 \tag{3}\end{align*}\]
Substituting equation \((3)\) into equation \((1)\) we get: \[\begin{aligned} y &= -\frac{3}{4}(0.64k - 9.6) + 30\\ y &= -0.48k + 37.2\end{aligned}\]
Therefore, the point \(W\) has coordinates \(( 0.64k - 9.6, -0.48k + 37.2)\).
We will now find two expressions for the length of \(QW\).
Using the distance formula we know \[QW = \sqrt{(0.64k - 9.6 - k)^2 + (-0.48k + 37.2 - 50)^2}\tag{4}\]
Another way to find the length \(QW\) is using the area of the parallelogram.
The length of \(PS = \sqrt{(30-0)^2 + (0-40)^2} = \sqrt{2500} = 50\), since \(PS > 0\).
\(PS\) is the base of the parallelogram and \(QW\) is the height. Therefore, \[\begin{align*} PS \times QW &= 1340\\ 50QW &= 1340\\ QW &= 26.8 \tag{5} \end{align*}\]
Now equating equations \((4)\) and \((5)\), we can solve for \(k\). \[\begin{aligned} \sqrt{(0.64k - 9.6 - k)^2 + (-0.48k + 37.2 - 50)^2} &= 26.8\\ (-0.36k - 9.6 )^2 + (-0.48k - 12.8)^2 &= 718.24\\ 0.1296k^2 + 6.912k + 92.16 + 0.2034k^2 + 12.288k + 163.84 &= 718.24\\ 0.36k^2 + 19.2k - 462.24 & = 0 \end{aligned}\]
Using the quadratic formula, we find \(k=18\) or \(k=-\frac{214}{3}\). Since \(Q(k,50)\) is in the first quadrant, we must have \(k > 0\) and so \(k=18\).
Therefore, the coordinates of \(Q\) and \(R\) are \(Q(18,50)\) and \(R(58,20)\).