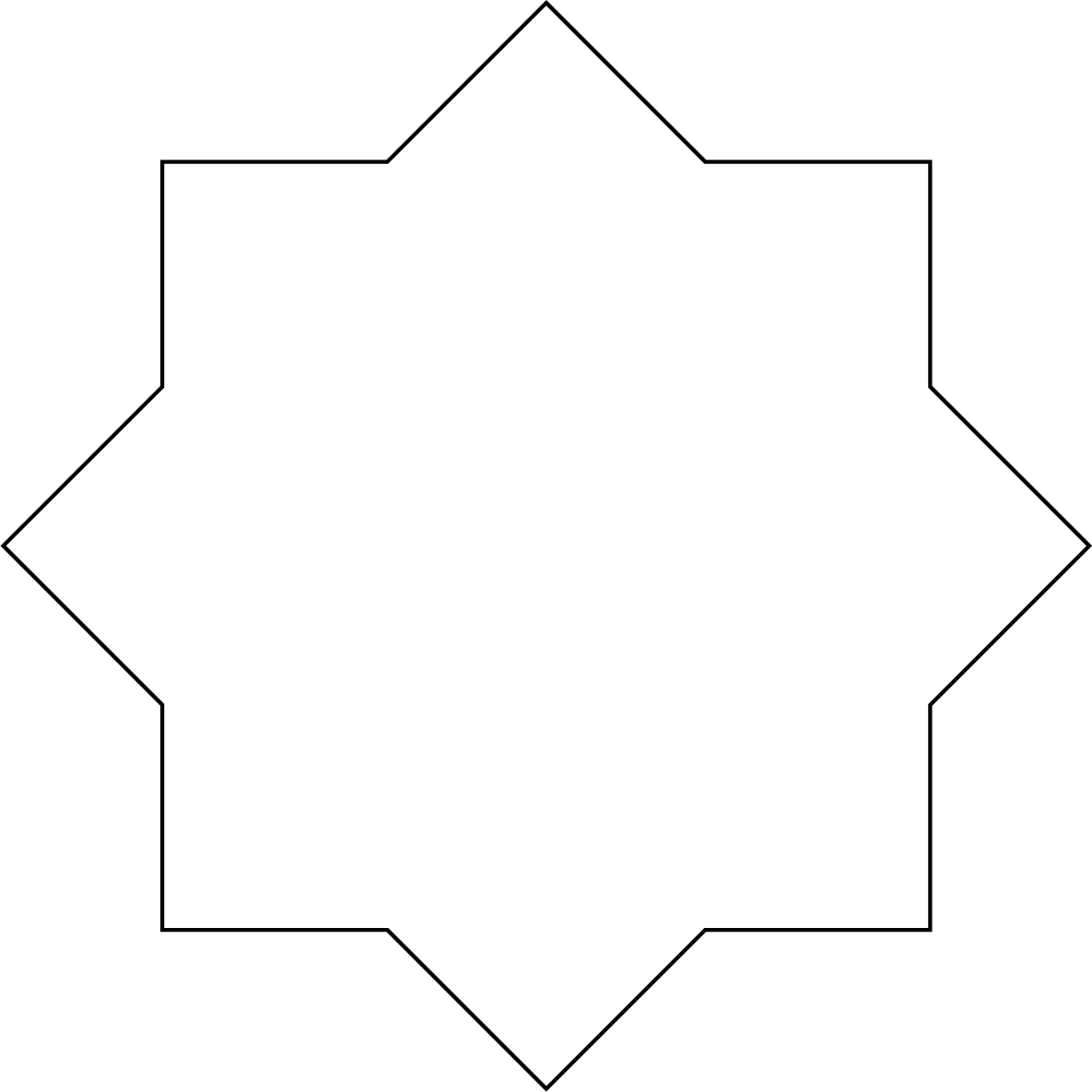

The Star of Lakshmi can be found in many places around the world. You can construct this shape by starting with two congruent squares on top of each other. (Two squares are congruent if they have the same side length.) Then imagine you have a pin in the centre of the square and you rotate the top square by \(45\degree\) (half of a quarter turn). The outline of the result would look like the following shape.

Fill in the table below with details about this shape.
| Number of sides | |
|---|---|
| Number of vertices | |
| Number of interior right angles | |
| Number of interior acute angles (angles that are less than \(90\degree\)) | |
| Number of lines of symmetry |
| Number of sides | \(16\) |
|---|---|
| Number of vertices | \(16\) |
| Number of interior right angles | \(8\) |
| Number of interior acute angles (angles that are less than \(90\degree\)) | \(0\) |
| Number of lines of symmetry | \(8\) |
Here are some notes about the answers.
A diagram of the Lakshmi star with its \(16\) vertices labelled \(A\) through \(P\) is below.

The interior angles at vertices \(A\), \(C\), \(E\), \(G\), \(I\), \(K\), \(M\), and \(O\) are all right angles, since they were originally parts of one of the squares used to construct the star.
Also, the interior angles at vertices \(B\), \(D\), \(F\), \(H\), \(J\), \(L\), \(N\), and \(P\) are all greater than \(90\degree\). In fact these angles are all greater than \(180\degree\) (a straight line). Note: angles that are greater than \(180\degree\) are called reflex angles.
Since we have now considered all \(16\) angles in the star, there are no interior acute angles.
Since the shape was formed by two squares, we can draw lines of symmetry between \(8\) pairs of opposite vertices as shown in the diagram below. We label these lines of symmetry as L1, L2, L3, L4, L5, L6, L7, and L8.
