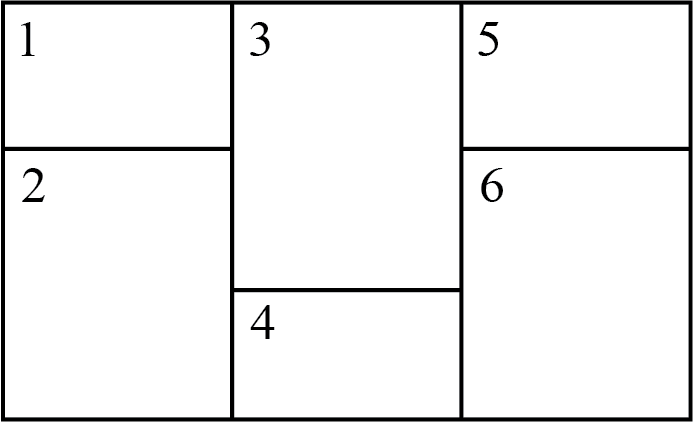

Martina and Zahra play a game where they take turns shading regions in the diagram shown.

On their turn, each player shades a region in the diagram that is not bordering another shaded region. After some number of turns, it won’t be possible to shade any more regions, and the game will be over. The winner is the player who shaded the last region.
Suppose Martina is the first player to shade a region. Two of the six regions are such that if she shades one of them on her first turn, then she can guarantee that she wins the game, regardless of what Zahra does on her turns. Which two regions are they?
Shading region \(3\) or region \(4\) first will guarantee that Martina wins the game. First we will show why this is true, and then we will show why shading any of the other regions first will not guarantee a win for Martina.
Notice that every region in the diagram borders region \(3\). So if Martina starts by shading region \(3\) then it will not be possible to shade any other region and the game will be over. Zahra will not even have a chance to take a turn and Martina will win the game.
Now, if Martina starts by shading region \(4\), then since regions \(2,~3,\) and \(6\) border region \(4\), Zahra will not be able to shade these regions. The only regions that Zahra will be able to shade are regions \(1\) or \(5\). Since these regions are not bordering each other, Zahra will shade one of these regions, then Martina will shade the other region and win the game.
Thus, we have shown that shading either region \(3\) or region \(4\) first will guarantee a win for Martina.
If Martina started by shading region \(1\), then Zahra would not be able to shade regions \(2\) or \(3\), so she would be left to choose between shading region \(4,~5\), or \(6\). Since region \(6\) borders regions \(4\) and \(5\), if Zahra shaded region \(6\) then Martina would not be able to shade any regions and Zahra would win the game. Thus, shading region \(1\) first does not guarantee a win for Martina.
Similarly, if Martina started by shading region \(5\), then Zahra would not be able to shade regions \(3\) or \(6\), so she would be left to choose between shading region \(1,~2\), or \(4\). Since region \(2\) borders regions \(1\) and \(4\), if Zahra shaded region \(2\) then Martina would not be able to shade any regions and Zahra would win the game. Thus, shading region \(5\) first does not guarantee a win for Martina.
If Martina started by shading region \(2\), then Zahra would not be able to shade regions \(1,~3,\) or \(4\), so she would be left to choose between shading region \(5\) or \(6\). Since regions \(5\) and \(6\) border each other, if Zahra shaded either one of them it would not be possible for Martina to shade any regions and Zahra would win the game. Thus, shading region \(2\) first does not guarantee a win for Martina.
Similarly, if Martina started by shading region \(6\), then Zahra would not be able to shade regions \(3,~4,\) or \(5\), so she would be left to choose between shading region \(1\) or \(2\). Since regions \(1\) and \(2\) border each other, if Zahra shaded either one of them it would not be possible for Martina to shade any regions and Zahra would win the game. Thus, shading region \(6\) first does not guarantee a win for Martina.
Therefore, regions \(3\) and \(4\) are the only regions that Martina can shade first in order to guarantee that she wins the game, regardless of what Zahra does on her turns.