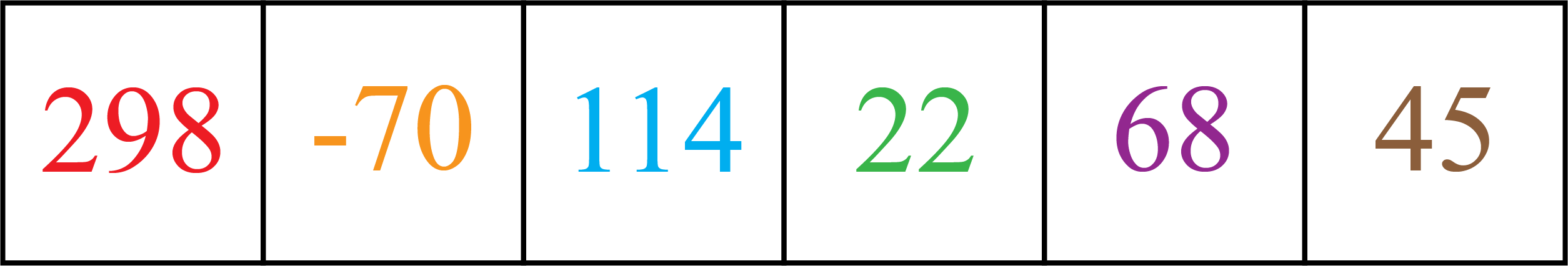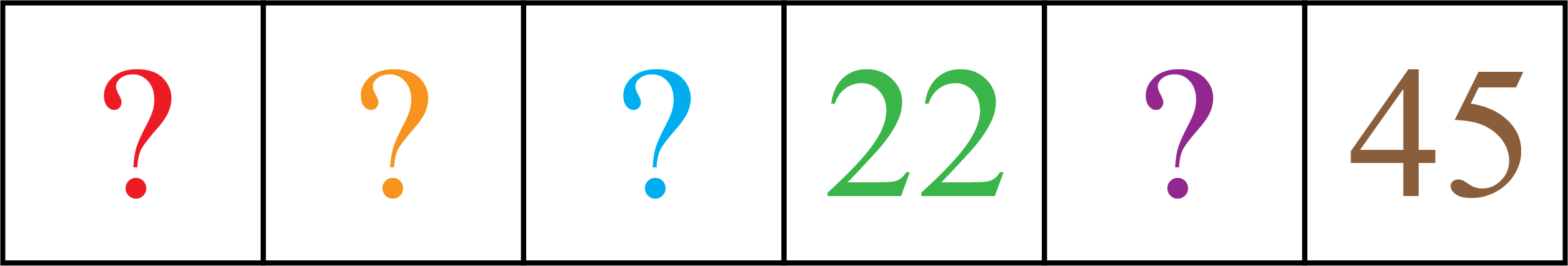

Jackie is making a sequence of six numbers using the following rules.
She choses any two numbers for the first two numbers.
The next four numbers are each the average of the previous two numbers.
After she creates the sequence, she tells her friend that the fourth number is \(22\) and the sixth number is \(45\). What numbers did Jackie choose for the first two numbers?
We give two solutions. Both will use the fact that if \(x\) is the average of two numbers \(y\) and \(z\), then \(\frac{y+z}{2}=x\), and it follows that \(y+z=2\times x\).
Solution 1
In the first solution, we solve the problem by working backwards.
Since the sixth number in the sequence is equal to the average of the two previous numbers, the sixth number must be the average of the fourth and fifth numbers. So, the sum of the fourth and fifth numbers must be \(2\) times the sixth number, or \(2\times 45 = 90\). Therefore, the fifth number is \(90 - 22 = 68\).
We now determine the third number. The fifth number in the sequence is the average of the third and fourth numbers. So, the sum of the third and fourth numbers is \(2\) times the fifth number, or \(2 \times 68 = 136\). Therefore, the third number is \(136 - 22 = 114\).
We now determine the second number. The fourth number in the sequence is the average of the second and third numbers. So, the sum of the second and third numbers is \(2\) times the fourth number, or \(2\times 22 = 44\). Therefore, the second number is \(44 - 114 = -70\).
We now determine the first number. The third number in the sequence is the average of the first and second numbers. So, the sum of the first and second numbers is \(2\) times the third number, or \(2\times 114 = 228\). Therefore, the first number is \(228 - (-70) = 228+70=298\).
Therefore, the first number is \(298\) and the second number is \(-70\).
Solution 2
We will now present a similar, but more algebraic solution.
Let \(a\) represent the first number in the sequence, \(b\) represent the second number in the sequence, \(c\) represent the third number in the sequence, and \(d\) represent the fifth number in the sequence. We again solve this problem by working backwards.
Since the sixth number in the sequence is equal to the average of the fourth and fifth numbers, we have \(45 = \frac{22+d}{2}\). Multiplying both sides by \(2\), we obtain \(22 + d = 45 \times 2 = 90\). Rearranging, \(d = 90 - 22 = 68\). Therefore, the fifth number in the sequence is \(68\).
We now determine the third number. Since the fifth number in the sequence is equal to the average of the third and fourth numbers, we have \(68 = \frac{c+22}{2}\). Multiplying both sides by \(2\), we obtain \(c +22 = 68 \times 2 = 136\). Rearranging, \(c = 136 - 22 = 114\). Therefore, the third number in the sequence is \(114\).
We now determine the second number. Since the fourth number in the sequence is equal to the average of the second and third numbers, we have \(22 = \frac{b+114}{2}\). Multiplying both sides by \(2\), we obtain \(b+114 = 22 \times 2 = 44\). Rearranging, \(b = 44 - 114 = -70\). Therefore, the second number in the sequence is \(-70\).
We now determine the first number. Since the third number in the sequence is equal to the average of the first and second numbers, we have \(114 = \frac{a+(-70)}{2}\). Multiplying both sides by \(2\), we obtain \(a +(-70) = 114 \times 2 = 228\). Rearranging, \(a = 228 +70 = 298\). Therefore, the first number in the sequence is \(298\).
Therefore, the first number is \(298\) and the second number is \(-70\).