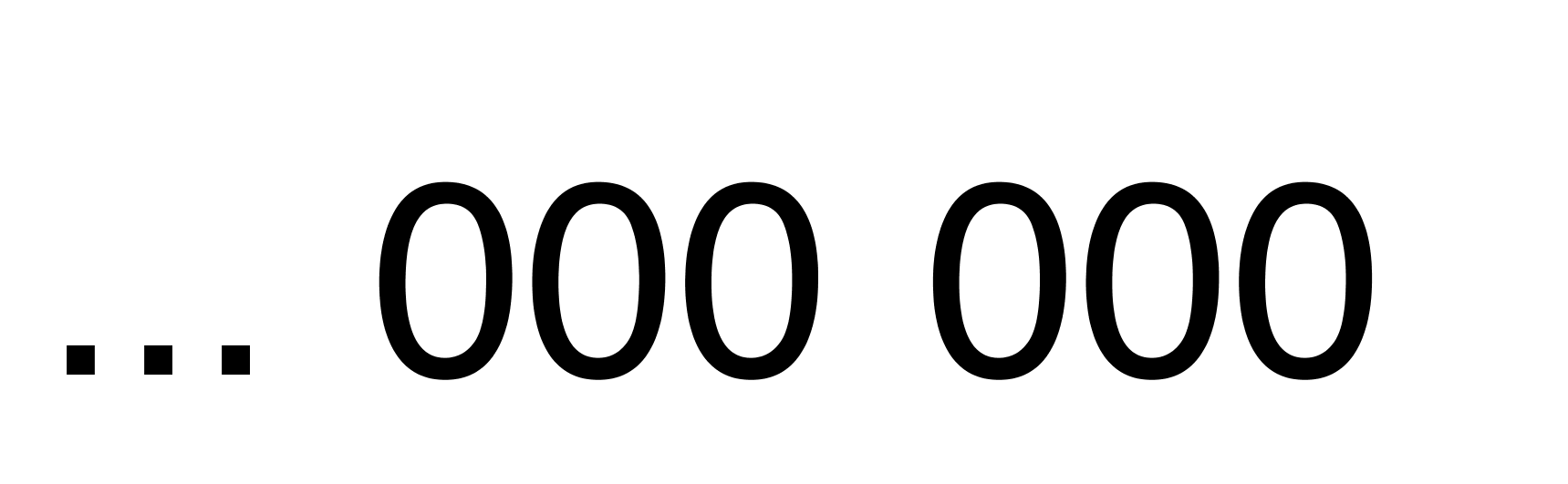

The product of the first seven positive integers is equal to \[7 \times 6\times 5\times 4\times 3\times 2\times 1= 5040\] Mathematicians will write this product as \(7!\). This is read as “\(7\) factorial”. So, \(7! = 7 \times 6\times 5\times 4\times 3\times 2\times 1= 5040\).
This factorial notation can be used with any positive integer. For example, \(11! = 11 \times 10 \times 9 \times \cdots \times 3 \times 2 \times 1 = 39\,916\,800\). The three dots “\(\cdots\)” represent the product of the integers between \(9\) and \(3\).
In general, for a positive integer \(n\), \(n!\) is equal to the product of the positive integers from \(1\) to \(n\).
Find the smallest positive integer \(n\) such that \(n!\) ends in exactly six zeros.
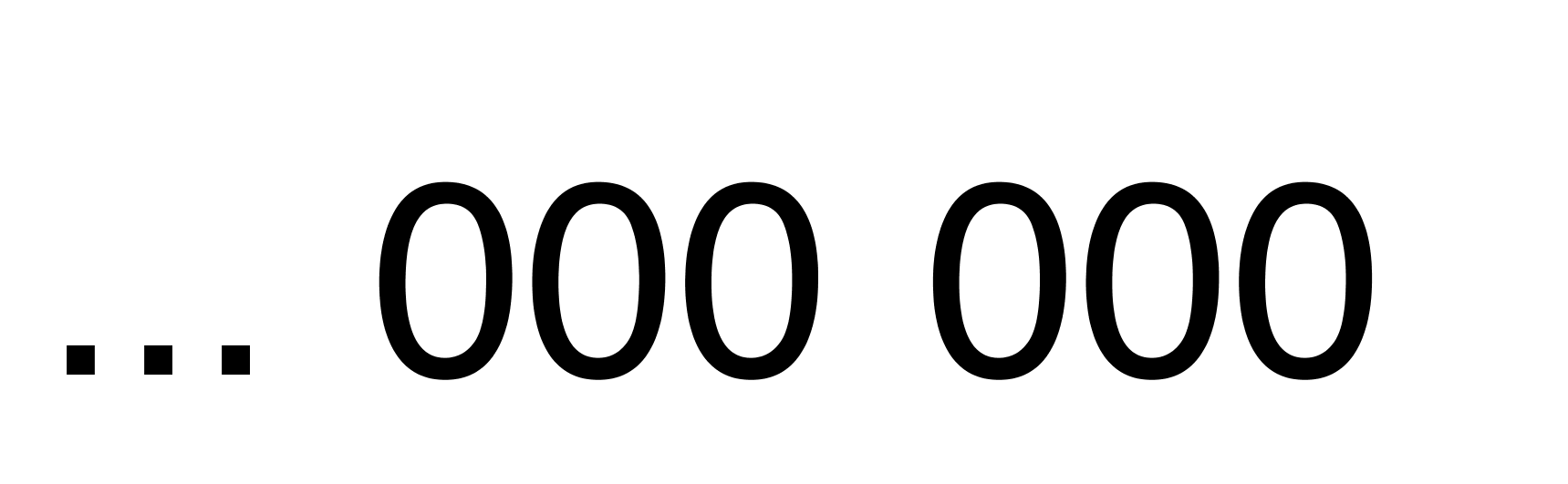
We start by examining the first few factorials: \[\begin{aligned} 1! &= 1\\ 2! &= 2 \times 1 = 2\\ 3! &= 3\times 2\times 1 = 6\\ 4! &= 4\times 3\times 2\times 1 = 24\\ 5! &= 5\times 4\times 3\times 2\times 1 = 120\\ 6! &= 6\times(5\times 4\times 3\times 2\times 1) = 6\times 5! = 6(120) = 720\\ 7! &= 7\times(6\times 5\times 4\times 3\times 2\times 1) = 7\times 6! = 7(720) = 5040\\ 8! &= 8\times(7\times 6\times 5\times 4\times 3\times 2\times 1) = 8\times 7! = 8(5040) = 40\,320\\ 9! &= 9\times(8\times 7\times 6\times 5\times 4\times 3\times 2\times 1) = 9\times 8! = 9(40\,320) = 362\,880\\ 10! &= 10\times(9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1) = 10\times 9! = 10(362\,880) = 3\,628\,800 \end{aligned}\]
These numbers are getting very large and soon will not fit on the display of a standard calculator. So, let’s look at what is going on.
We observe that \(5!\) ends in \(0\) and \(10!\) ends in \(00\). Notice that the number of zeros at the end of the number increased by one at each of \(5!\) and at \(10!\). Why is this?
A zero is added to the end of a positive integer when we multiply by \(10\). Multiplying a number by \(10\) is the same as multiplying a number by \(2\) and then by \(5\), or by \(5\) and then by \(2\), since \(2\times 5 = 10\) and \(5\times 2=10\). We must determine the next time we multiply by \(2\) and \(5\) (in some order), to know the next time the number of zeros at the end of the number increases again. Every time we multiply by an even positive integer we are multiplying by at least one more \(2\). In the integers from \(1\) to \(n\), there are less multiples of \(5\). So, each multiple of \(5\) will affect the number of zeros at the end of the product.
Multiplying by \(11\), \(12\), \(13\), and \(14\) increases the number of \(2\)s we multiply by but not the number of \(5\)s. So the number of zeros at the end of the product does not change. The next time we multiply by a \(5\) is when we multiply by \(15\) since \(15 = 5\times 3\). So \(15!\) will end in exactly three zeros, \(000\).
Multiplying by \(16\), \(17\), \(18\), and \(19\) increases the number of \(2\)s we multiply by but not the number of \(5\)s. So the number of zeros at the end of the product does not change. The next time we multiply by a \(5\) is when we multiply by \(20\) since \(20 = 4\times 5\). So \(20!\) will end in exactly four zeros, \(0000\).
Multiplying by \(21\), \(22\), \(23\), and \(24\) increases the number of \(2\)s we multiply by but not the number of \(5\)s. The next time we multiply by a \(5\) is when we multiply by \(25\). In fact, multiplying by \(25\) is the same as multiplying by \(5\) twice since \(25 = 5\times 5\). So when we multiply by \(25\), we will increase the number of zeros on the end of the product by two. So \(25!\) will end in exactly six zeros, \(000\,000\).
Therefore, the smallest positive integer \(n\) such that \(n!\) ends in exactly six zeros is
\(25\). (It could be noted that \(26!\), \(27!\), \(28!\), and \(29!\) also end in six zeros.)
For the curious, \[24!=620\,448\,401\,733\,239\,439\,360\,000\] and \[25!=15\,511\,210\,043\,330\,985\,984\,000\,000\]