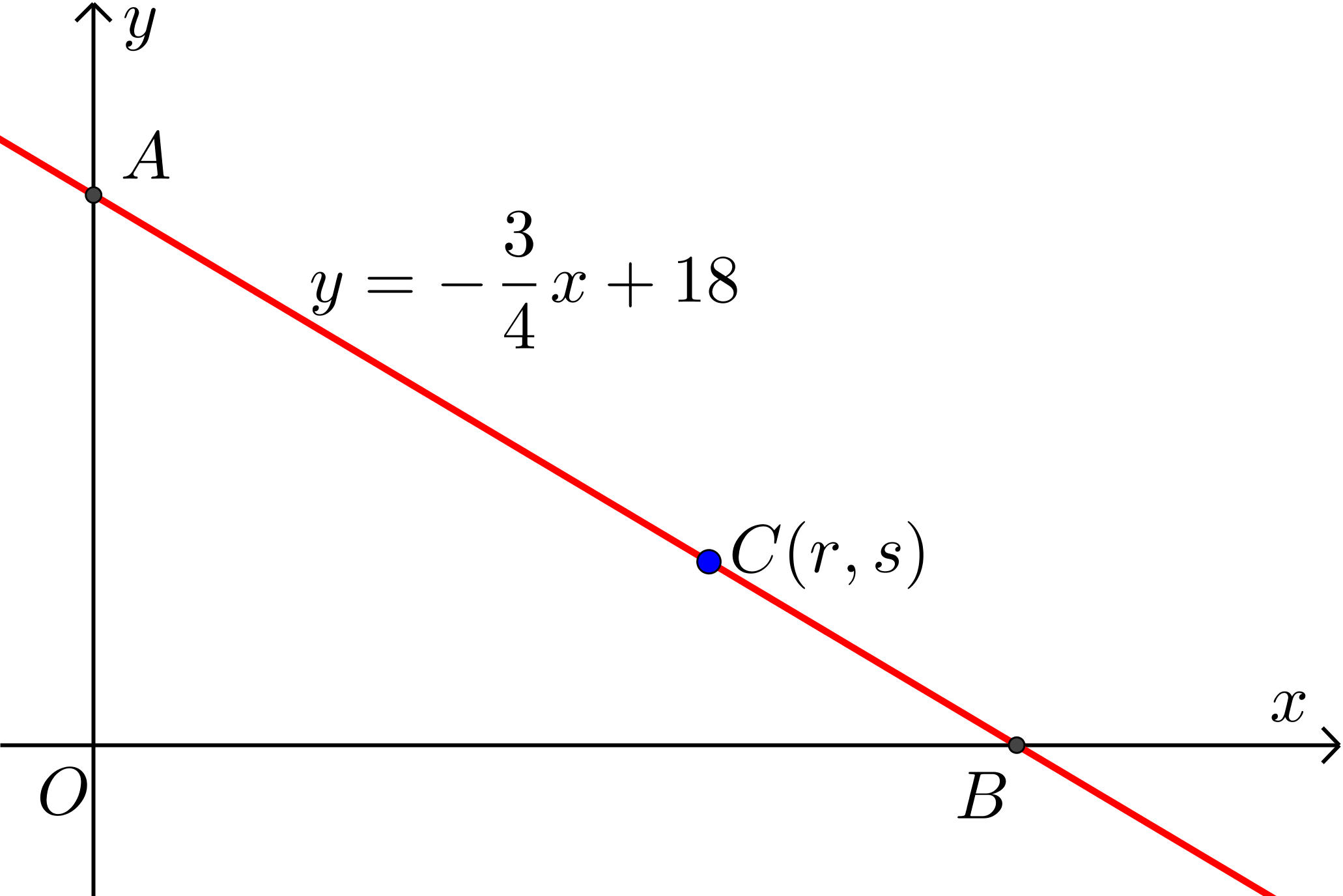

The line with equation \(y = -\frac{3}{4}x + 18\) crosses the positive \(x\)-axis at point \(B\) and the positive \(y\)-axis at point \(A\). The origin, \(O\), and points \(A\) and \(B\) form the vertices of a triangle.
Point \(C(r,s)\) lies on the line segment \(AB\) such that the area of \(\triangle AOB\) is three times the area of \(\triangle COB\).
Determine the values of \(r\) and \(s\).

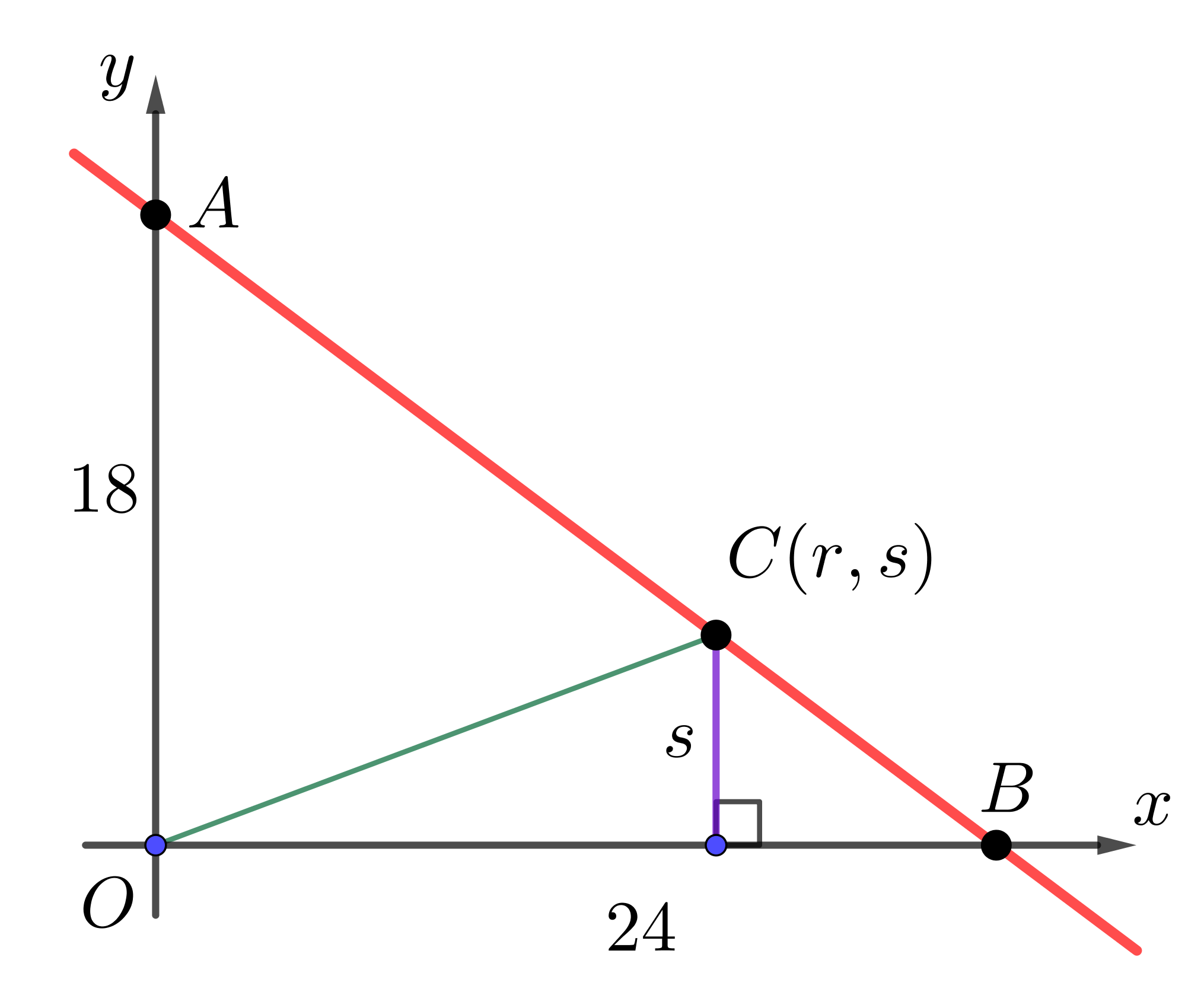
The equation of the line is written in the form \(y=mx+b\), where \(b\) is the \(y\)-intercept of the line. Thus, the \(y\)-intercept of the line with equation \(y=-\frac{3}{4}+18\) is 18, and \(OA = 18\).
To determine the \(x\)-intercept of the line, we set \(y=0\) to obtain \(0 = -\frac{3}{4}x + 18\). Solving, we have \(\frac{3}{4}x = 18\), and so \(x = 24\). Thus, \(OB=24\).
We drop a perpendicular from \(C\) to \(OB\). The base of \(\triangle COB\) is \(OB = 24\), and since \(C\) has \(y\)-coordinate \(s\), the height of \(\triangle COB\) is \(s\).
We now present two solutions to the problem.
Solution 1:
Since \(\triangle AOB\) is a right-angled triangle with base \(OB = 24\) and height \(OA = 18\), using the formula \(\text{area} = \frac{\text{base}\times\text{height}}{2}\), we have \(\text{area of }\triangle AOB = \frac{24\times 18}{2} = 216\).
Since the area of \(\triangle AOB\) is three times the area of \(\triangle COB\), \(\text{area of }\triangle COB = \frac{1}{3} (\text{area of }\triangle AOB) = \frac{1}{3}(216) = 72\).
Thus, \(\triangle COB\) has area \(72\), base \(OB = 24\), and height \(s\).
Using the formula \(\text{area} = \frac{\text{base}\times\text{height}}{2}\), we have \[\begin{aligned} \text{area of }\triangle COB &= \frac{OB\times s}{2}\\ 72 &= \frac{24\times s}{2}\\ 72 &= 12s\\ s &=6 \end{aligned}\]
Since \(C(r,s)\) lies on the line with equation \(y = -\frac{3}{4}x + 18\) and \(s=6\), we have \[\begin{aligned} 6 &= -\frac{3}{4}r + 18\\ \frac{3}{4}r &= 12\\ r &=16 \end{aligned}\]
Therefore, \(r=16\) and \(s= 6\).
Solution 2:
\(\triangle AOB\) and \(\triangle COB\) have the same base, \(OB\). If two triangles have the same base, then the areas of the triangles are proportional to the heights of the triangles.
Since the area of \(\triangle AOB\) is three times the area of \(\triangle COB\), then the height of \(\triangle AOB\) is three times the height of \(\triangle COB\). In other words, the height of \(\triangle COB\) is \(\frac{1}{3}\) the height of \(\triangle AOB\).
We know that \(\triangle AOB\) has height \(OA = 18\) and \(\triangle COB\) has height \(s\). Therefore, \(s = \frac{1}{3}(OA) = \frac{1}{3}(18) = 6\).
Since \(C(r,s)\) lies on the line with equation \(y = -\frac{3}{4}x + 18\) and \(s=6\), we have \[\begin{aligned} 6 &= -\frac{3}{4}r + 18\\ \frac{3}{4}r &= 12\\ r &=16 \end{aligned}\] Therefore, \(r=16\) and \(s= 6\).
Notice that in the second solution, it was actually unnecessary to find the length of \(OB\), as this was never used.
Extension:
Can you find the coordinates of point \(D\) on line segment \(AB\) so that the area of \(\triangle AOD\) is equal to the area of \(\triangle COB\), thus creating three triangles of equal area? How are the points \(A\), \(D\), \(C\), and \(B\) related?