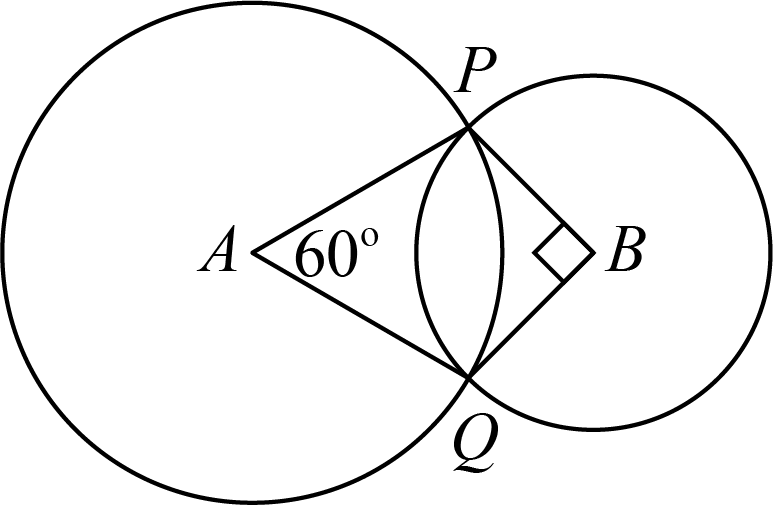

Two circles, one with centre \(A\) and one with centre \(B\), intersect at points \(P\) and \(Q\) such that \(\angle PAQ=60^\circ\) and \(\angle PBQ=90^\circ\).

If the area of the circle with centre \(A\) is \(48\,\text{m}^2\), what is the area of the circle with centre \(B\)?
Let \(c\) be the radius of the circle with centre \(A\), in metres, and \(d\) be the radius of the circle with centre \(B\), in metres. Then join \(P\) to \(Q\).
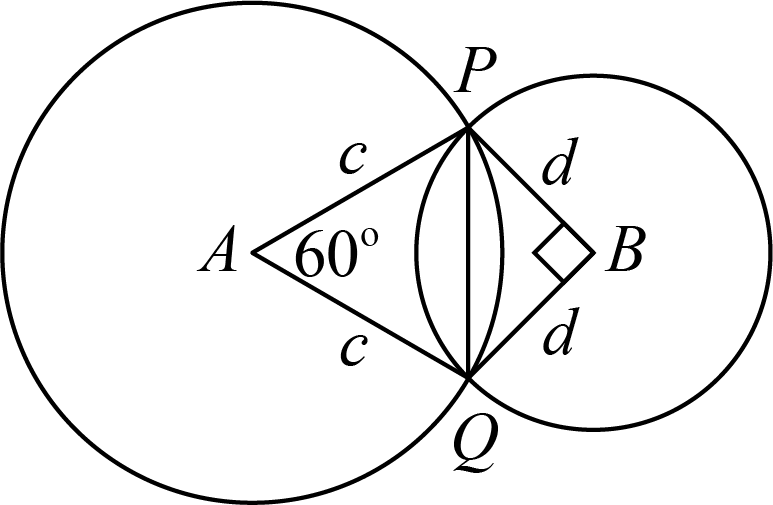
We will determine the length of \(PQ\) in terms of \(c\) and then in terms of \(d\) in order to find a relationship between \(c\) and \(d\).
Consider \(\triangle APQ\). Since \(AP = AQ = c\), \(\triangle APQ\) is isosceles and so \(\angle APQ = \angle AQP\). Since \(\angle PAQ = 60^{\circ}\), \(\angle APQ = \angle AQP = \frac{180^{\circ} - 60^{\circ}}{2} = 60^{\circ}\). Therefore, \(\triangle APQ\) is equilateral and \(PQ = AP = AQ = c\).
Consider \(\triangle BPQ\). We are given that \(\angle PBQ = 90^{\circ}\). Therefore, \(\triangle BPQ\) is a right-angled triangle. The Pythagorean theorem tells us that \(PQ^2 = BP^2 + BQ^2 = d^2 + d^2 = 2d^2\).
We have \(PQ = c\) and \(PQ^2 = 2d^2\). Therefore, \(c^2 = 2d^2\).
The area of the circle with centre \(B\) and radius \(d\) is \(\pi d^2\).
The area of the circle with centre \(A\) and radius \(c\) is \(\pi c^2\). We know this area is equal to \(48\,\text{m}^2\). Then, \[\begin{aligned} 48 &= \pi c^2\\ 48 &= \pi (2d^2)\\ 48 &= 2 \pi d^2\\ 24 &= \pi d^2 \end{aligned}\] Therefore, the area of the circle with centre \(B\) is \(24\,\text{m}^2\).